Gli acidi e basi deboli sono, insieme ai gas,
i cavalli di battaglia dell’esame di stechiometria.
Sono gli argomenti con più margine di attenzione.
ACIDI E BASI DEBOLI – COMPARAZIONE FRA FORTE E DEBOLE
Una soluzione acquosa di 0,1 l contiene 0,03 moli
di HCl e HClO4. Si calcoli il pH. Due acidi forti si
dissociano completamente e le moli di ioni idronio
sono pari alle moli iniziali degli acidi pesati prima
di metterli in soluzione.
In soluzione, la concentrazione di acido forte
non esiste; si trasforma tutto in ione idronio.
\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} HCl\to Cl^{-}+H^{+}\\ \\ HClO_{4}\to ClO_{4}^{-}+H^{+}\\ \\ [H^{+}]_{f}=[HCl]_{i}+[HClO_{4}]_{i} \end{matrix}
Il ph della soluzione sarà:
\!\!\!\!\!\!\begin{matrix} ph:\\ \\ -log(\frac{(0,03+0,03)mol}{0,1l})=\\ \\ =0,222 \end{matrix}
Abbiamo preso le moli di acido pesate, le
abbiamo sommate e diluite per farne
l’argomento del logaritmo e calcolare il ph.
Invece, fra un acido ed una base forte basterà
fare la differenza e calcolare il pH con le moli
rimanenti. Le cose si complicano quando si
passa alle specie deboli.
DEFINIZIONE DI ACIDI FORTI E DEBOLI
Dicesi acido forte una specie che in soluzione
esiste solamente in forma di ione idronio, tale
che la concentrazione totale di ione idronio è
pari alla somma totale delle moli pesate di tutti
gli acidi forti fratto il volume della soluzione.
Peso sulla bilancia analitica l’acido forte, e
conoscendo il peso molecolare ne calcolo le
moli. Allo stesso modo calcolo le moli di altri
acidi forti. Il ph della soluzione risultante sarà
il logaritmo negativo delle moli totali di questi
acidi fratto il volume.
Allo stesso modo, una base forte è una specie
che in soluzione esiste solo in forma di ione idrossile.
Si ricordi che:
- per acidi forti si intende Ka >> 1 e α ≈ 1
- per basi forti, invece, si ha Kb >>1 e α ≈ 1
ESEMPI DI NEUTRALIZZAZIONI FRA SPECIE FORTI
Nel caso di acidi e basi forti la situazione è molto
semplice. Innanzitutto, si fa la sottrazione delle
moli, poi si calcola la concentrazione della specie
residua e si stabilisce il ph:
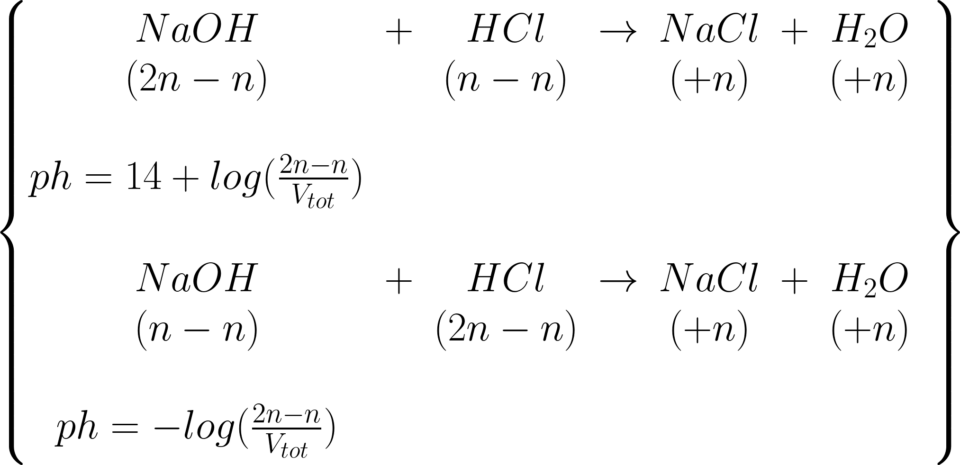
Ad una soluzione 0,150 l di NaOH 0,045 M si
aggiungono 0,150 l di HCL 0,0392 M. Si calcoli il ph.
In questo caso, gli acidi sono stati pesati per
fare delle soluzioni indipendenti, cosicchè,
invece di risalire alle moli dai pesi, li ricaviamo
dalle concentrazioni delle soluzioni di partenza.
Ora, la traccia dice che di queste soluzioni
vengono prelevate due aliquote che vengono
messe in una nuova soluzione, e ne cerca il ph.
Vanno, però prima calcolare le moli. Bisogna
immaginare HCl come sinonimo di H+ e NaOH
come sinonimo di OH–.
Nella formula logaritmica le concentrazioni
sono moli mascherate. Un chimico ragiona
sempre e solo in moli.
\large \begin{matrix} ph=14-pOH\\ \end{matrix}
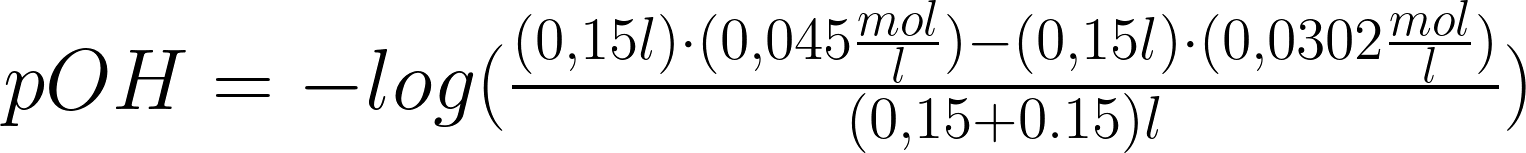
\large \begin{matrix} ph=11,86\\ \end{matrix}
Se, invece, le concentrazioni fossero invertite, allora il
ph risultante sarebbe:
\large \begin{matrix} pH: \end{matrix}
\!\!\!\!\!\!\!\!\!\scriptsize\begin{matrix} -log(\frac{(0,15\not l)\cdot (0,045\frac{mol}{\not l})-(0,15)\not l \cdot (0,0302\frac{mol}{\not l})}{(0,15+0.15)\not l})=\\ \end{matrix}
\large \begin{matrix} pH=2,13 \end{matrix}
Clicca qui:
Acidi e basi forti esercizi.
Per gli acidi e basi deboli la situazione è meno
immediata. Dobbiamo porre vari casi generali.
Acido forte in difetto rispetto la base debole
Le reazioni indipendenti sono:
\!\!\!\!\!\!\!\!\! \left\{\begin{matrix} HA\; \to H^{+}\; +A^{-}\\ (n-n)\; (+n)\; (+n)\\ \\ BOH\; \rightleftharpoons B^{+}\; +OH^{-}\\ (2n-X)\; (+X)\; (+X)\\ \end{matrix}\right.
Avviene prima una neutralizzazione preliminare,
in seguito regna l’equilibrio della specie residua:
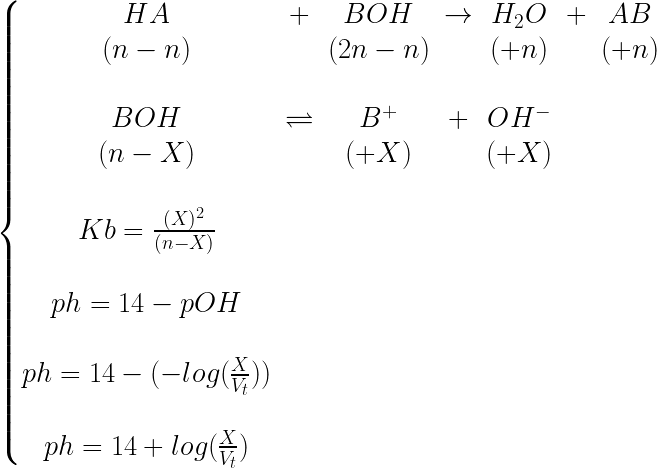
Perché non avviene lo spostamento di equilibrio?
Ma una neutralizzazione che è una reazione diretta?
Siccome l’acido è forte, “tira” la base debole fino
a neutralizzazione.
Base forte in difetto rispetto l’acido debole
Le reazioni indipendenti sono:
\!\!\!\!\!\!\!\!\!\left\{\begin{matrix} BOH\; \to B^{+}\; +OH^{-}\\ \!\!\!\!\!\!\!\!\!\!\!\!(n-n)\; (+n)\; (+n)\\ \\ HA\; \rightleftharpoons H^{+}\; +OH^{-}\\ (2n-X)\; (+X)\; (+X) \end{matrix}\right.
Lo stesso discorso vale anche qui. Si ha, prima di
tutto, una neutralizzazione preliminare, e poi il
pH sarà determinato dalla specie predominante:
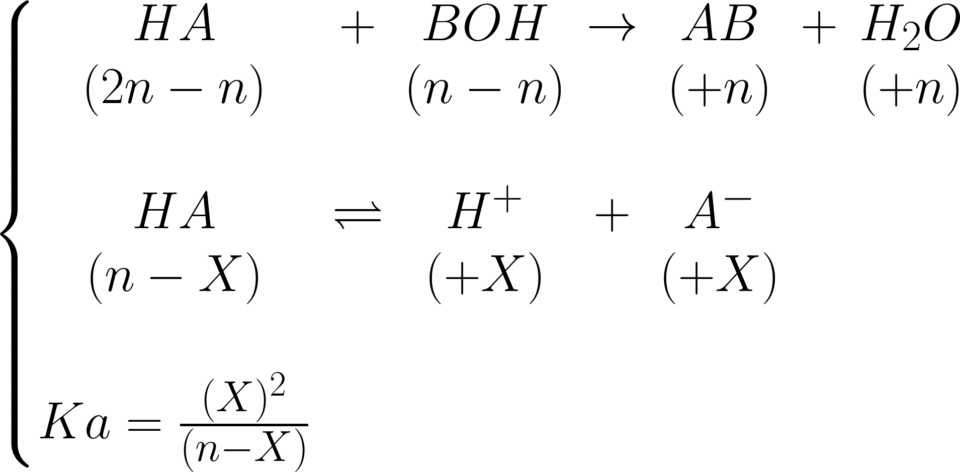
\!\!\!\!\!\!\large \left\{\begin{matrix} ph=-log([H^{+}])\\ \\ ph=-log(\frac{X}{V_{t}}) \end{matrix}\right.
Clicca qui:
Acidi e Basi deboli esercizi
ACIDI E BASI DEBOLI –
GRADO DI DISSOCIAZIONE α
Quindi, il grado di dissociazione non serve solo per “fotografare” Le Chatelier in azione, ma anche per
risolvere problemi di reazioni acido/base di equilibrio.
La trattazione matematica è la stessa dello spostamento dell’equilibrio. Ciò che varia, se pur formalmente, è la definizione:
\alpha =\frac{[H^{+}]}{[HA]}=\frac{n_{dissociate}}{n_{iniziali}}
Clicca qui:
ACIDI E BASI DEBOLI – ESERCIZI CON α
