INTRODUZIONE
Questa è la pagina di approfondimenti Kp.
Sono svolti solamente tre esercizi per
approfondire l’argomento degli equilibri
propedeutico di Le Châtelier.
APPROFONDIMENTI Kp – ESERCIZIO 1
Si calcoli la Kp dopo che 1,50 g di NH3 in 1,50 l
di volume sono scaldati fino a 448 K, sapendo
che l’ammoniaca si è dissociata del 15%.
La traccia può apparire sibillina, ma trasformato
in matematica diventa intuitivo:
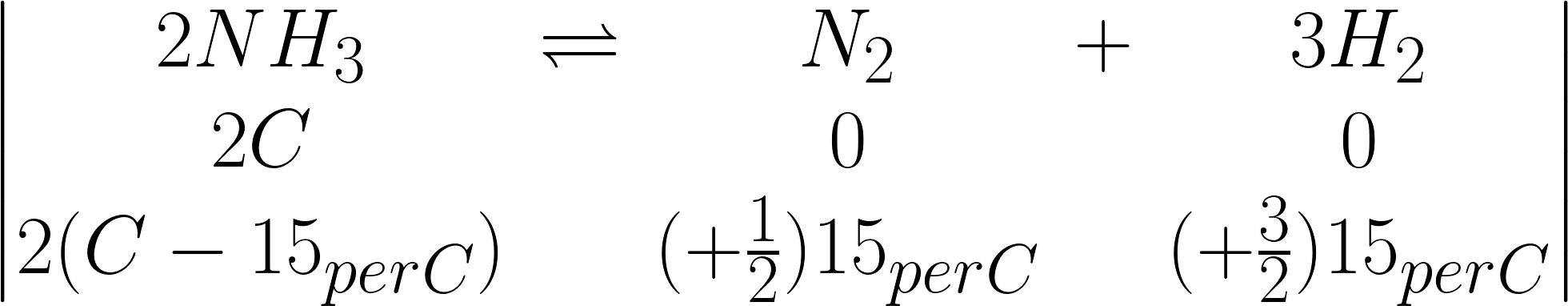
\Large \begin{matrix} K_{p}=\frac{[P_{N_{2}}][P_{H_{2}}]^{3}}{[P_{NH_{3}}]^{2}}\end{matrix}
Lo schema taglia la testa al toro sul significato
della traccia. In italiano non è mai immediato
il senso della traccia… Bando alle ciance!
Bisogna calcolare le moli iniziali di ammoniaca,
ricavarne il 15% e dividerlo secondo gli indici
stechiometrici.
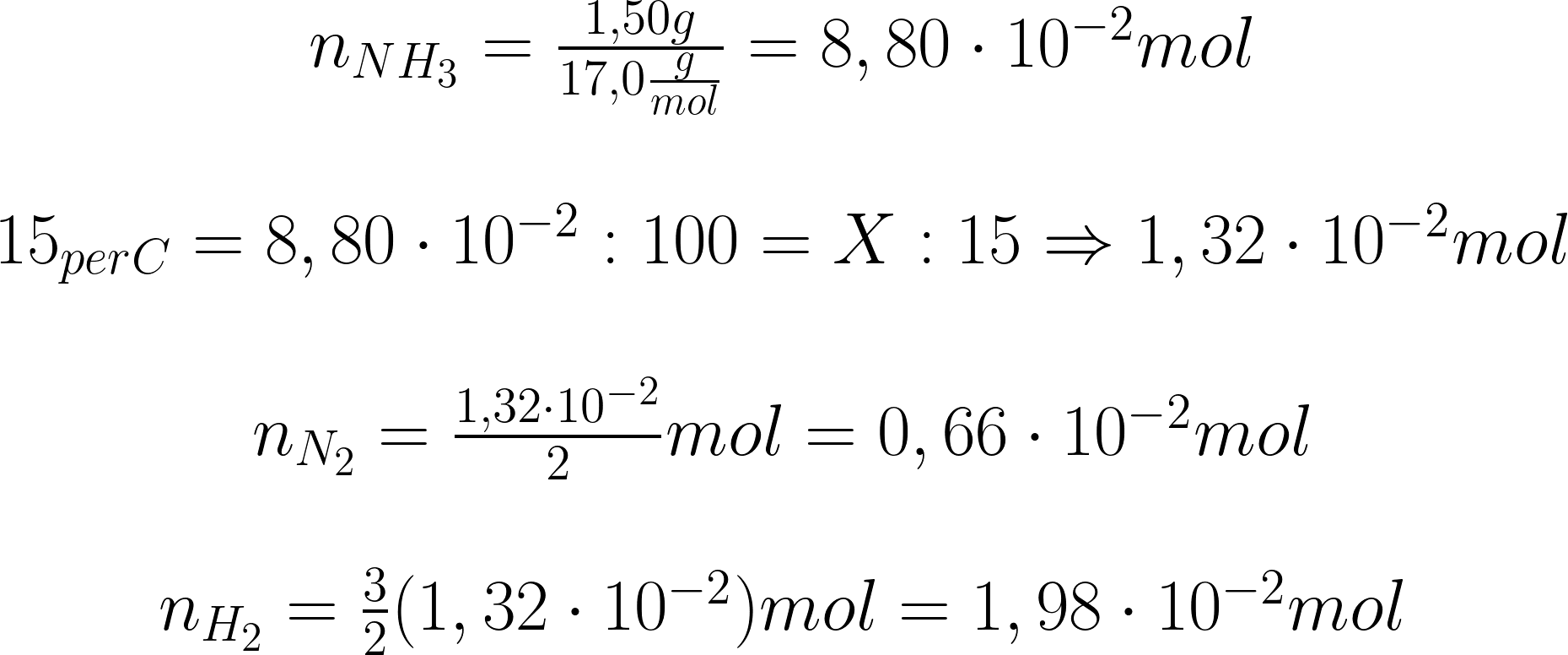
Per comprendere i prossimi passaggi è opportuno
fare un ulteriore schema:
\begin{matrix} P_{NH_{3}}\!=\!(\frac{R\cdot T}{V})(C\!-\!15_{\%})\\ \\ \!\!\!\!\!\!P_{H_{2}}\!=\!(\frac{R\cdot T}{V})(\frac{3}{2})15_{\%}\\ \\ \!\!\!\!\!\!P_{N_{2}}\!=\!(\frac{R\cdot T}{V})(\frac{1}{2})15_{\%} \end{matrix}
\!\!\!\!\!\begin{matrix} (C-15_{\%})\!=\!7,5\!\cdot \!10^{-2}mol\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\frac{R\cdot T}{V}\!=\!25,50\frac{atm}{mol} \end{matrix}
Ponendo le moli di ammoniaca all’equilibrio si
procede al calcolo delle pressioni parziali.
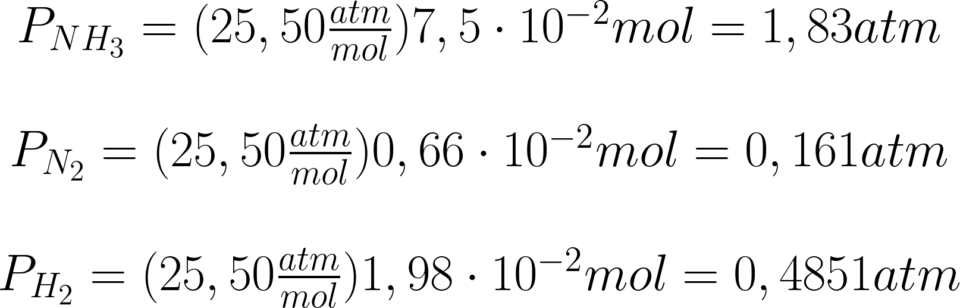
\large \!\!\!\!\!\!\!\!\begin{matrix} \!\!\!\!\!\!\!\!\!K_{p}\!=\!\frac{[P_{N_{2}}][P_{H_{2}}]^{3}}{[P_{NH_{3}}]^{2}}\\ \\ K_{p}\!=\!\frac{[0,161atm][0,4851atm]^{3}}{[1,83atm]^{2}}\\ \\ \!\!\!K_{p}\!=\!5,48\!\cdot \!10^{-3}atm ^{2} \end{matrix}
Si noti come la percentuale di dissociazione
esprima un equilibrio di reazione.
APPROFONDIMENTI Kp – ESERCIZIO 2
Sia un recipiente di capacità 0,500 l riempito
con pari volumi di monossido di carbonio e cloro,
il tutto riscaldato fino a 600 K. La pressione iniziale
è 1,98 atm. La Kp è 0,450 atm-1. Si calcolino le
masse di tutte le specie all’equilibrio.
Fissiamo i concetti:
\!\!\!\!\!\!\!\!\!\! \begin{matrix} \!\!\!\!\!\!\!\!\!\!CO\!+\!Cl_{2}\!\rightleftharpoons \!COCl_{2}\\ \\ K_{p}\!=\!\frac{P_{COCl_{2}}}{P_{CO}\cdot P_{Cl_{2}}}\!=\!0,450\,atm^{-1} \end{matrix}
Ricordandoci però che a volume e temperatura
costanti i rapporti in pressioni sono pari ai
rapporti in volume:
\Large \begin{matrix} \frac{P_{CO}}{P_{Cl_{2}}}=\frac{V_{CO}}{V_{Cl_{2}}} \end{matrix}
Abbiamo:
\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \frac{X}{(P_{CO}-X)\cdot (P_{Cl_{2}}-X)}\!=\!0,450\,atm^{-1}\\ \\ \!\!\!\!\!\!\!\!\!(P_{CO}-X)\!=\!(P_{Cl_{2}}-X)\\ \\ \!\!\!\!\!\!\!\!\!\frac{X}{(P_{CO}-X)^{2}}\!=\!0,450\,atm^{-1} \end{matrix}
La pressione totale all’inizio è 1,98 atm, cumulativa
di due pressioni parziali uguali, quindi 0,99+0,99
per cui abbiamo:
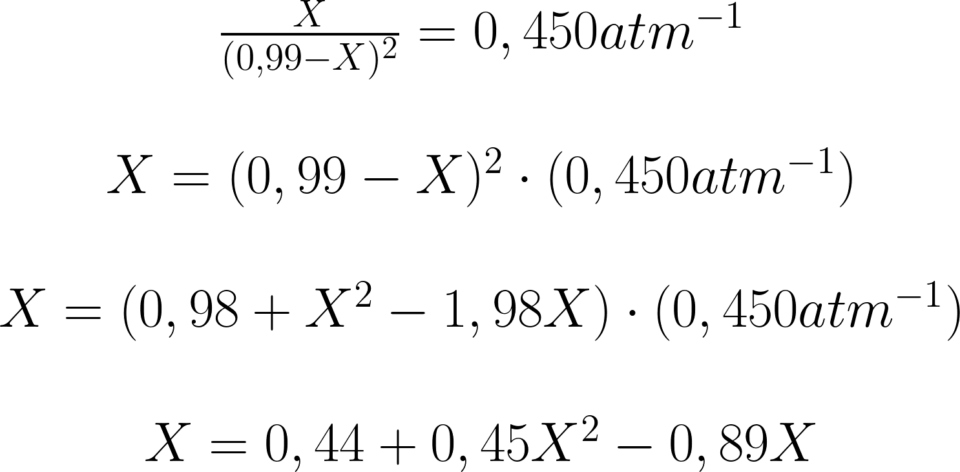
\!\!\!\!\!\!\!\!\!\!\!\begin{matrix} 0,45X^{2}\!-\!1,89X\!+\!0,44\!=\!0\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!X\tfrac{2}{1}\!=\!\frac{-b\pm \sqrt{(b^{2}-4\cdot a\cdot c)}}{2\cdot a}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!X\tfrac{2}{1}\!=\!\frac{1,89\pm (1,66)}{0,9} \end{matrix}
Si scarta la radice superiore a 0,99 che non ha
senso fisico (la pressione dissociata è maggiore
della pressione iniziale), rimane 0,25 atm da cui:
\large \!\!\!\!\!\!\!\begin{matrix} \frac{0,25atm}{0,74^{2}}\!=\!0,450atm^{-1} \end{matrix}
Le masse sono:
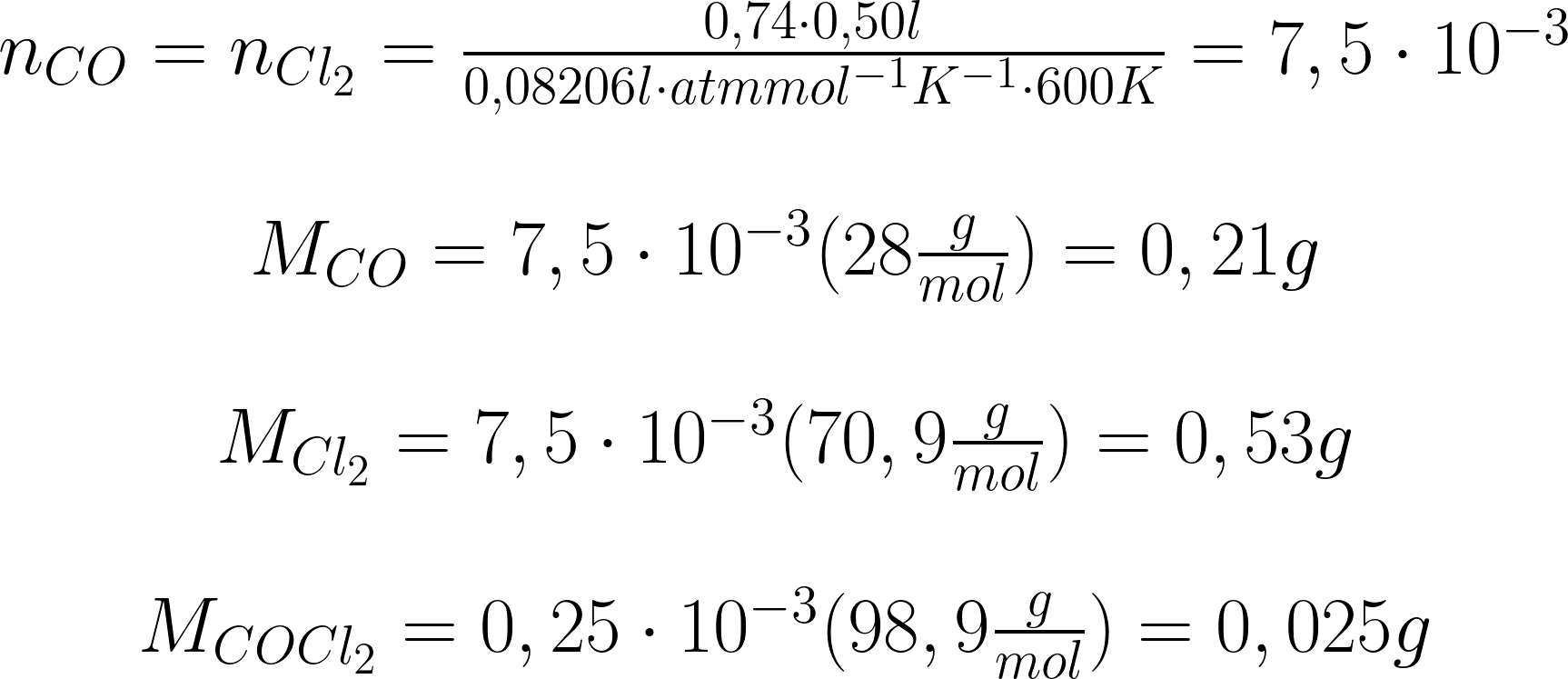
APPROFONDIMENTI Kp – ESERCIZIO 3
Il biossido di azoto (NO2) è contenuto in un recipiente
di 1,00 l alla temperatura di 298 K. La sua pressione è
di 0,105 atm, però quando viene riscaldato a 843 K la pressione del sistema diventa 0,360 atm e si instaura
il seguente equilibrio:
\Large \!\!\!\!\!\begin{matrix} NO_{2}\! \rightleftharpoons \!NO\!+\!\frac{1}{2}O_{2} \end{matrix}
Si calcoli la Kp di tale equilibrio. Riassumendo:
\small \!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!K_{p}\!=\!\frac{P_{NO}\cdot (P_{O_{2}})^{\frac{1}{2}}}{(P_{NO_{2}})}\!=\!X\\ \\ P_{NO_{eq}}\!+\!P_{O_{2}}\!+\!P_{NO_{2}}\!=\!0,360\,atm \end{matrix}
A volume e moli costanti i rapporti in temperatura
sono pari ai rapporti in pressioni, quindi possiamo
calcolare la pressione di NO2 al momento in cui si
dissocia (la Peq).
\Large \!\!\! \begin{matrix} \!\!\frac{P_{in.} }{P_{f.} }\!=\!\frac{T_{ in. } }{T_{ f. } }\\ \\ \!\!\!\!\frac{0,105 atm}{X}\!=\!\frac{298K}{843K}\\ \\ X\!=\!\frac{843K\cdot 0,105 atm}{298K} \end{matrix}
Da cui risulta che la pressione di NO2 all’equilibrio
è 0,297 atm.
Da qui la pressione totale si è ripartita secondo gli
indici stechiometrici, quindi abbiamo:
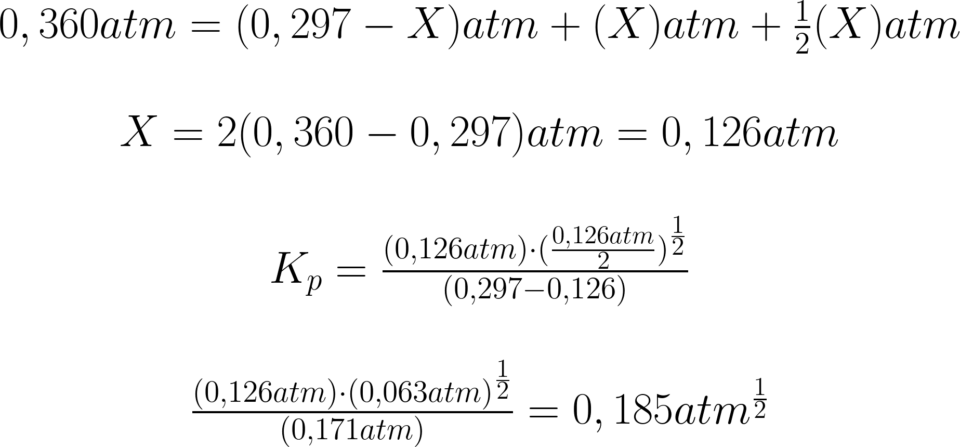
La pagina di approfondimenti finisce qui. Per
approfondimenti sugli NXOY si guardi il video
della A2C:
