Le titolazioni acido-base non sono
tanto diverse dalle titolazioni redox
già affrontate nelle sezioni precedenti.
INTRODUZIONE
La titolazione è una neutralizzazione
il cui scopo è conoscere il “titolo”
(la concentrazione) della specie
in soluzione di cui si conosce
la reazione chimica col titolante.
La neutralizzazione avviene
a completezza quando la soluzione
cambia di colore il quale testimonia
che si è raggiunti il
punto di equivalenza. Si possono
avere tre casi a seconda del prodotto
di titolazione formato:
- base coniugata che determina un pH>7
- acqua cosicché il pH=7
- acido coniugato che determina un pH<7
TITOLAZIONI ACIDO-BASE – CASO 1
10,0 cm3 0,25 M di acido dicloroacetico
sono stati utilizzati per titolare 0,45 M
di potassa caustica.
La Keq della titolazione è 1,6 • 1011.
Si calcoli il titolo della potassa ed
il pH finale.
La dissociazione della potassa
caustica è una reazione diretta,
mentre, per l’acido dicloroacetico
c’è una Ka = 1,6 • 10-3.
Ovviamente, tale costante si
ignora perché nella neutralizzazione
la soda “tira” a completezza
la reazione.
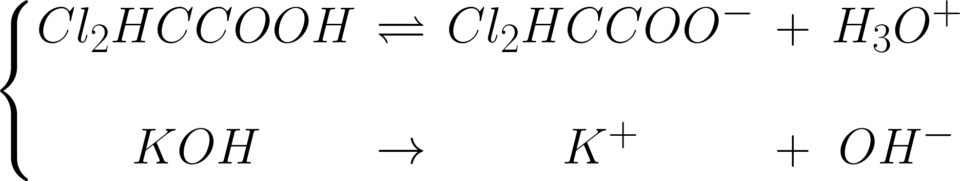
La reazione di titolazione è:
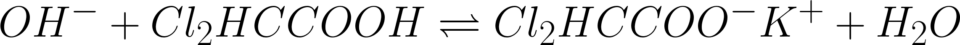
(KOH non esiste in soluzione)
10,0 cm3 equivalgono a 10,0 ml
ossia 10,0 • 10-3 l La titolazione
cessa quando moli del titolante
equivalgono alle moli del titolato,
quindi i litri di soda sono:
\footnotesize \begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!0,25\,M\,10,0\cdot 10^{-3}l=0,45\,M\cdot \textbf{X}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!0,25\frac{mol}{{\color{Red} l}}10^{-2}{\color{Red} l}=0,45\frac{mol}{l}\cdot \textbf{X} \end{matrix}
\large \begin{matrix} X=\frac{0,25\cdot 10^{-2}{\color{Red} mol}}{0,45\frac{{\color{Red} mol}}{l}}\\ \\ X=0,00555=\\ 5,5\cdot 10^{-3}l \end{matrix}
La soda si è trasformata in acqua,
ma qual è il pH del carbossilato
formato? É un errore pensare
che essendo la titolazione una
neutralizzazione, il pH finale sia
sempre 7. A primo acchito,
la molecola residua è la base
coniugata, il carbossilato, quindi
il pH risultante sarà basico?
Scopriamolo!
Per cominciare ricalcoliamo la
concentrazione perché il volume
è cambiato:
\scriptsize \begin{matrix} \!\!\!\!\!\!\!\!\![Cl_{2}HCCOO^{-}]=\frac{0,25(\frac{mol}{{\color{Red} l}})\cdot 10,0\cdot 10^{-3}{\color{Red} l}}{(10,0+5,55)\cdot 10^{-3}l}\\ \end{matrix}
\begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\![Cl_{2}HCCOO^{-}]=\frac{2,5\,mol}{15,55l}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\![Cl_{2}HCCOO^{-}]=0,160\,M \end{matrix}
Ora procediamo col calcolo del pH:
\begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!1,6\cdot 10^{11}=\frac{[Cl_{2}HCCOO^{-}]}{[OH^{-}]\cdot[HCCOOH]}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!1,6\cdot 10^{11}=\frac{[Cl_{2}HCCOO^{-}]}{X^{2}}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!X=\sqrt{\frac{[Cl_{2}HCCOO^{-}]}{1,6\cdot 10^{11}}}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!X=\sqrt{\frac{0,160}{1,6\cdot 10^{11}}}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\![OH^{-}]=\sqrt{0,1\cdot 10^{-11}} \end{matrix}
Il pH finale sarà:
\begin{matrix} \!\!\!\!\!\!\!\!\!\!\!pOH=-log(\sqrt{0,1\cdot 10^{-11}})\\ \\ \!\!\!\!\!\!\!\!\!pOH=6\\ \\ \!\!\!\!\!\!\!\!\!pH=14-6=8 \end{matrix}
Si badi bene, è stata usata la
costante di titolazione, ma con
la Kb del carbossilato l’esito
sarebbe stato lo stesso.
TITOLAZIONI ACIDO-BASE – CASO 2
8,0 cm3 0,12 M di acido cloridrico
sono stati utilizzati per titolare
0,50 M di soda caustica.
La Keq della titolazione è
1,8 • 1014. Si calcoli il titolo
della potassa ed il pH finale.
Sia l’acido cloridrico che la soda
caustica idrolizzano con reazione
diretta.
\large \!\!\!\!\!\!\!\!\!\!\!\left\{\begin{matrix} \!\!\!\!\!\!\!HCl\!\to \!Cl^{-}\!+\!H_{3}O^{+}\\ \\ NaOH\!\to \!Na^{+}\!+\!OH^{-} \end{matrix}\right.
La reazione di titolazione è:
\large \begin{matrix} \!\!\!\!\!\!\!\!\!OH^{-}\!+\!H^{+}\rightleftharpoons 2H_{2}O \end{matrix}
\!\!\!\!\!\!\!\!\! \footnotesize \begin{matrix} \!\!\!0,12\,M \cdot 8,0\cdot 10^{-3}l=0,50\,M \cdot \textbf{X}\\ \\ \!\!\!\!\!\!0,96\frac{mol}{{\color{Red} l}}\cdot 10^{-3}{\color{Red} l}=0,50\frac{mol}{l}\cdot \textbf{X} \end{matrix}
\large \begin{matrix} \textbf{X}\!=\frac{0,96\cdot 10^{-3}{\color{Red} mol}}{0,50\frac{{\color{Red} mol}}{l}}\\ \\ X\!=1,92\cdot 10^{-3}l \end{matrix}
Non vi sono basi coniugate,
per cui il pH finale è 7.
Siamo a neutralità.
TITOLAZIONI ACIDO-BASE – CASO 3
2,6 • 10-3 l di ammoniaca vengono
titolati da 0,20 M 1,8 • 10-3 l di acido
cloridrico. La Keq della titolazione è
1,8 • 109. Si calcolino il titolo di
ammoniaca titolata ed il pH finale.
\large \!\!\!\!\!\!\!\!\!\! \left\{\begin{matrix} HCl\!\to \!Cl^{-}\!+\!OH^{-}\\ \\ NH_{3}\!\rightleftharpoons \!NH_{4}^{+}\!+\!H_{3}O^{+}\\ \end{matrix}\right.
La reazione di titolazione è:
\!\!\!\!\!\!\!\!\!\begin{matrix} NH_{3}\!+\!HCl\!\to \!NH_{4}^{+}\!+\!Cl^{-} \end{matrix}
Da qui si denota che la titolazione non porterà
ad un pH finale neutro poiché lo ione ammonio
formato è un acido debole.
\!\!\!\!\!\!\!\!\!\!\!\!\footnotesize \begin{matrix} 0,20M(1,8\cdot 10^{-3}l)\!=\!(2,6\cdot 10^{-3}l)\textbf{X}\\ \\ \!\!\!0,36\frac{mol}{{\color{Red} l}}(10^{-3}{\color{Red} l})=(2,6\cdot 10^{-3}l)(\textbf{X}) \end{matrix}
\large \!\!\!\!\!\!\!\!\!\begin{matrix} \textbf{X}=\frac{0,36\cdot {\color{Red} 10^{-3}}{mol}}{2,6\cdot {\color{Red} 10^{-3}}l}\\ \\ X=0,138\approx 0,14M \end{matrix}
Quindi, per titolare l’ammoniaca
abbiamo usato acido cloridrico
0,20 molare 1,8 cm3. L’ammoniaca,
di cui si conosceva solo il volume
(2,6 cm3), grazie all’equazione
abbiamo potuto calcolarne il titolo
pari a 0,14 M.
Per prima cosa, siccome l’acido
cloridrico ha tirato con sé tutta
l’ammoniaca abbiamo che le moli
totali di ammonio sono pari a quelle
di ammoniaca iniziale, ma diluita.
Bisogna, quindi, procedere col
ricalcolo della concentrazione.
\large \!\!\!\!\!\!\!\!\!\!\begin{matrix} [NH_{4}^{+}]\!=\!\frac{0,14(\frac{mol}{{\color{Orange} }l})\cdot \!2,6 \!\cdot \!{\color{Red} 10^{-3}}{\color{Orange} }\not l}{(2,6+1,8)\!\cdot \!{\color{Red} 10^{-3}}\not l}\\ \\ \!\!\![NH_{4}^{+}]=\frac{(0,364)mol}{4,4l}\\ \\ \!\!\![NH_{4}^{+}]=0,08272\\ \approx 8,3 \cdot 10^{-2}M \end{matrix}
Ora procediamo col calcolo del pH:
\!\!\!\!\!\!\!\!\!\large\begin{matrix} 1,8\cdot \!10^{9}\!=\!\frac{[NH_{4}^{+}]}{[H_{3}O^{+}][NH_{3}]}\\ \\ 1,8\cdot \!10^{9}\!=\!\frac{[NH_{4}^{+}]}{X^{2}}\\ \\ X^{2}\!=\!\frac{8,3 \cdot \!10^{-2}}{1,8\cdot 10^{9}} \end{matrix}
\large \!\!\!\!\!\! \begin{matrix} X=\sqrt{\frac{8,3}{1,8}(\cdot 10^{-11}})=\\ 0,68\cdot 10^{-5}M \end{matrix}
Il pH sarà:
\large \!\!\!\!\!\!\!\! \begin{matrix} \!\![H_{3}O^{+}]=0,7\cdot 10^{-5}\\ \\ pH\!=\!-log(0,7\!\cdot \!10^{-5})\\ \\ \!\!pH=5,17 \end{matrix}
Conoscendo, invece, la Ka dello
ione ammonio si può procedere
in modo analogo invertendo
l’incognita:
\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \!\!\!NH_{4}^{+}\rightleftharpoons NH_{3}+H_{3}O^{+}\\ \\ \!\!\!Ka=\frac{X^{2}}{[NH_{4}^{+}]}\\ \\ \!\!\!X=\sqrt{[NH_{4}^{+}]\cdot Ka}\\ \\ [H_{3}O^{+}]\!=\!\sqrt{(5,5)(8,3)\!\cdot \!10^{-12}} \end{matrix}
\large \!\!\!\!\!\!\begin{matrix} [H_{3}O^{+}]=0,68\cdot 10^{-5}\\ \approx 0,7\cdot 10^{-5}M\\ \end{matrix}
In questo terzo caso, invece,
abbiamo un pH finale acido.
