Vi sono tre casi essenziali che coinvolgono
acidi e basi polifunzionali:
1) Se la Ka1>>1 (o pKa1<<0) si vede l’equilibrio
della Ka2 eventualmente competitiva con le
specie presenti;
2) Altrimenti, quando ka1<<1 (o pKa1>>0) si
trascura la seconda dissociazione e si valutano
i contributi delle specie presenti;
3) Nel caso 1) la concentrazione protonica è
molto bassa, si considera l’acqua non solo il
solvente, ma anche un acido debole.
ACIDI E BASI POLIFUNZIONALI – ESERCIZI
ACIDO BIPROTICO FORTE
Si calcoli il pH di una soluzione acquosa 0,2 M
di acido solforico.
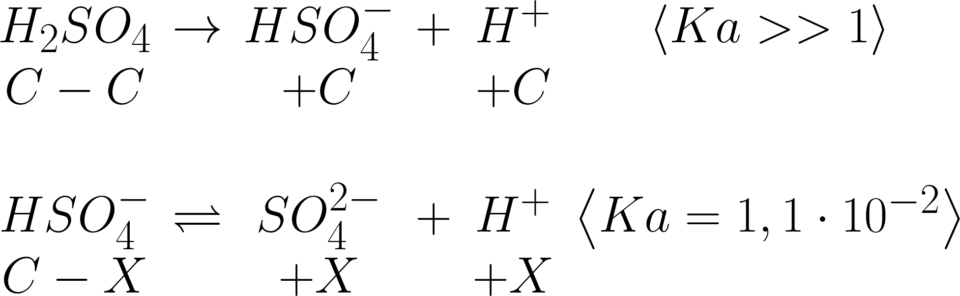
L’acido solforico è molto forte e si dissocia
completamente. Il primo equilibrio, quindi,
lo si può scartare poiché la base coniugata
si comporta ancora da acido, questa volta
debole, ed innesca un nuovo equilibrio con la
concentrazione iniziale di acido che non c’è più.
\large \begin{matrix} Ka=\frac{X^{2}}{C-X}\\ \\ \!\!\!\!\!\!\!\!\!C\!\cdot \!Ka\!-\!X\!\cdot \!Ka\!-\!X^{2}\!=\!0\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\!X^{2}\!+\!(Ka)X\!-\!CKa\!=\!0 \end{matrix}
Sostituiamo i valori:
\scriptsize \begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!X^{2}\!+\!(1,1\!\cdot \!10^{-2})X\!-\!(0,2)1,1\!\cdot \!10^{-2}\!=\!0&\\ \end{matrix}
\begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!\frac{-1,1\cdot 10^{-2}\pm \sqrt{(1,1\cdot 10^{-2})^{2}+4(2,2) 10^{-3}}}{2}\\ \\ \!\!\!X_{1/2}=0,04172\cup \textit{n.s.f.} \end{matrix}
Lo ione idrogeno solfato ha si tutta la concentrazione
iniziale di acido solforico, ma bisogna ricordarsi
che lo ione idronio rilasciato nella prima idrolisi
c’è ancora, quindi:
\begin{matrix} pH=-log(C-X)\\ \\ \!\!\!\!\!\!\!\!\!\!pH\!=\!-log(0,2+0,04172)\\ \\ pH=0,617 \end{matrix}
In alternativa:
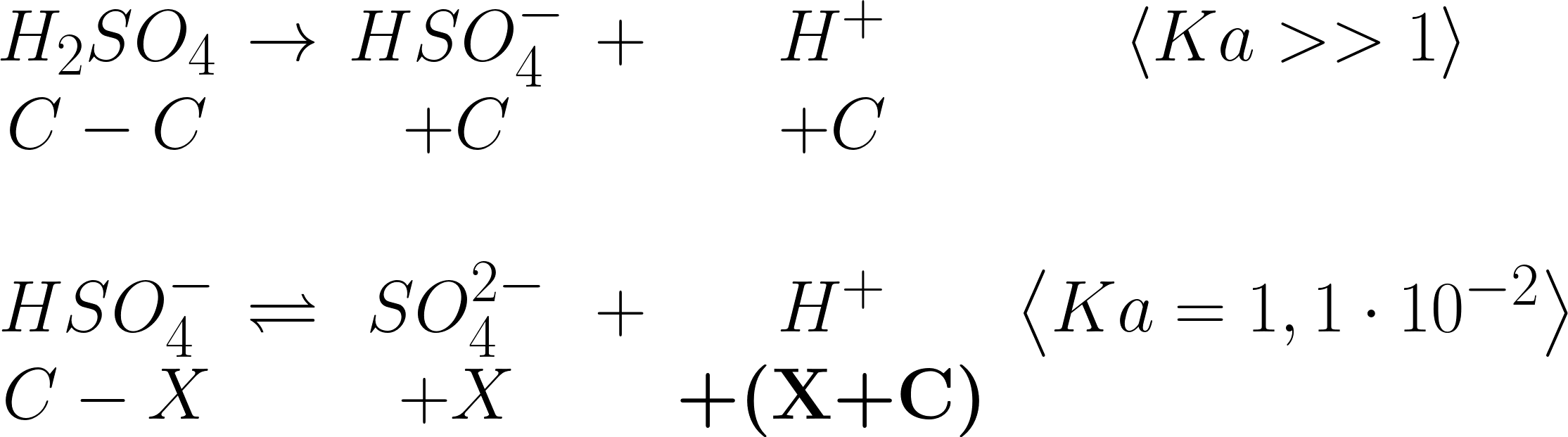
\small \begin{matrix} Ka=\frac{(X)(C+X)}{C-X}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!X^{2}\!+\!X(0,2\!+\!Ka)\!-\!0,2Ka\!=\!0\\ \\ X=\textbf{0,24172} \end{matrix}
ACIDO BIPROTICO DEBOLE
Si trovi il pH di una soluzione acquosa 0,10 M
di acido solfidrico, le cui costanti sono:
Ka1=1,0×10-7
Ka2=1,1×10-13
Gli equilibri sono:
\footnotesize \begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!H_{2}S\!\rightleftharpoons \!HS^{-}\!+\!H^{+}Ka\!=\!10^{-7}\\ \textit{si trascura:}\\ \!\!\!\!\!\!\!\!\!\!\!\!{\color{Red} HS^{-}\!\rightleftharpoons \!S^{2-}\!+\!H^{+}Ka\!=\!1,1\!\cdot \!10^{-13}}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\color{Red} H_{2}O\!\rightleftharpoons \!H^{+}\!+\!OH^{-}Ka\!=\!10^{-14}} \end{matrix}
La secondo dissociazione è molto simile
all’autoprotolisi per cui la trascuriamo.
\large \begin{matrix} \frac{X^{2}}{C{\color{Red} -X}}=Ka\\ \textit{siccome}\\ \!\!\!\!\!\!\!\!\!\!\! Ka<10^{-4}\cup C >10^{-2}\\ \\ \frac{X^{2}}{C}=1,0\cdot 10^{-7}\\ \\ \!\!\!\!\!\!\!X\!=\!\sqrt{0,10\!\cdot \!10^{-7}}\\ \\ \!\!\!\!\!\!\!pH\!=\!-log(10^{-4})\!=\!4 \end{matrix}
ACIDI E BASI POLIFUNZIONALI –
EQUILIBRI SIMULTANEI
Dato un volume ignoto di acido perclorico dal
titolo 10-7 M, Si calcoli il pH. Ragionando come
negli esercizi precedenti, il pKa è molto forte
(>>1) quindi si trascura l’autoprotolisi, le specie
deboli eventualmente presenti e si fa il logaritmo
negativo che uscirebbe 7…
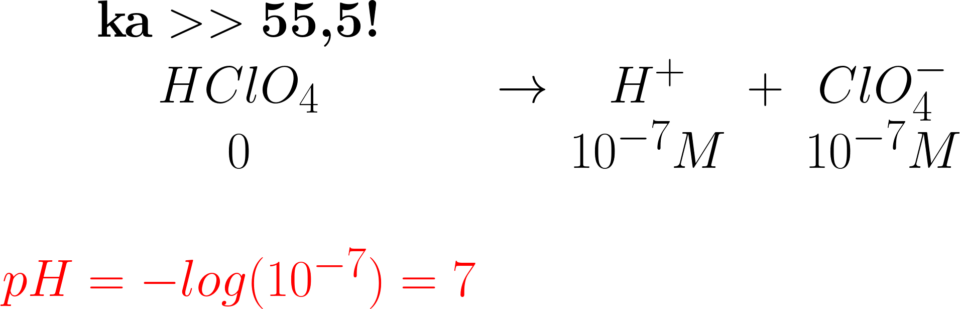
Un acido forte aggiunto in acqua può mai lasciare
il pH in ambiente neutro? Proviamo ad aggiungere nell’autoprotolisi lo ione idronio aggiunto:
\large \begin{matrix} \textbf{prima}\\ \!\!\!\!\!k_{w}=[H^{+}]_{i}\cdot [OH^{-}]_{i}\\ \\ \textbf{dopo}&\\ \!\!\!\!\!k_{w}=[H^{+}]_{f}\cdot [OH^{-}]_{f}\\ \\ C_{H_{f}^{+}}>10^{-7}\\ \\ C_{OH_{f}^{-}}<10^{-7} \end{matrix}
Proviamo a costruire un equazione.
(H+acido + XH+ dell’autroprotolisi) per (OH–
dell’autoprotolisi – X della sua retrocessione):
\small \begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!k_{w}=[10^{-7}+X]\cdot [10^{-7}-X]\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!10^{-14}\!+\!10^{-7}(X\!-\!X)\!-\!X^{2}\!=\!0\\ \\ \!X^{2}\!=\!10^{-14}\\ \\ X=10^{-7} \end{matrix}
Non è andata. Allora ritentiamo.
(H+acido +H+Kw) per (OH– dell’autoprotolisi –
X della sua retrocessione):
\begin{matrix} \!\!\!\!\!\!\!\!\!2\!\cdot\!(10^{-7})(10^{-7}\!-\!X)\!=\!K_{W} \end{matrix}
\footnotesize \begin{matrix} \!\!\!\!\!\!\!\!\!2\!\cdot \!(10^{-14})\!-\!2\!\cdot \!(10^{-7})C\!-\!K_{W}\!=\!0\\ \\ \!\!\!\!\!\!\!\!\!\!-2\!\cdot \!(10^{-7})C\!+\!10^{-14}\!\cdot \!(2-1)\!=\!0 \end{matrix}
\begin{matrix} \!\!\!\!\!\!pH\!=\!-log(\frac{10^{- {\color{Red}14 }\;7}}{2\!\cdot \!{\color{Red}10^{- 7}}})\!=\! {\color{Red}6,30 } \end{matrix}
Il pH è troppo basso, non può essere.
La X verifica l’autoprotolisi, pH è inferiore a 7,
ma chimicamente ancora non è sperimentale.
10-7 vale per ioni a diluzione diluita, senza altre
specie. Qui l’acqua svolge ruolo di “acido debole”,
per cui ragioniamo come un normale equilibrio:
\small \begin{matrix} \!\!\!\!\!\!k_{eq}=\frac{[H^{+}][OH^{-}]}{[H_{2}O]}\\ \\ \!\!\!\!\!\!\textbf{Aggiungo un acido forte}\\ \\ \!\!\!\!\!\!k_{eq}=\frac{(10^{-7})(X)}{H_{2}O}\\ \\ \!\!\!\!\!\!Kw=[10^{-7}][X]\\ \!\!\!\!\!\!\textbf{non può essere 7, allora } \end{matrix}
\begin{matrix} \!\!\!\!\!\!k_{w}\!=\![10^{-7}\!+\!X]\!\cdot \![X]\\ \\ \!\!\!\!\!\!X^{2}\!+\!10^{-7}X\!-\!10^{-14}\!=\!0\\ \\ \!\!\!\!\!\!X_{1}^{2}\!=\!\frac{-10^{-7}\pm \sqrt{(10^{-7})^{2}\!+\!4(10^{-14})}}{2}\\ \\ \!\!\!\!\!\!X_{1}^{2}\!=\!\frac{-10^{-7}\pm (10^{-7})\sqrt{1+4}}{2}\\ \\ \!\!\!\!\!\!X_{1}^{2}\!=\!0,62\!\cdot \!10^{-7}M \end{matrix}
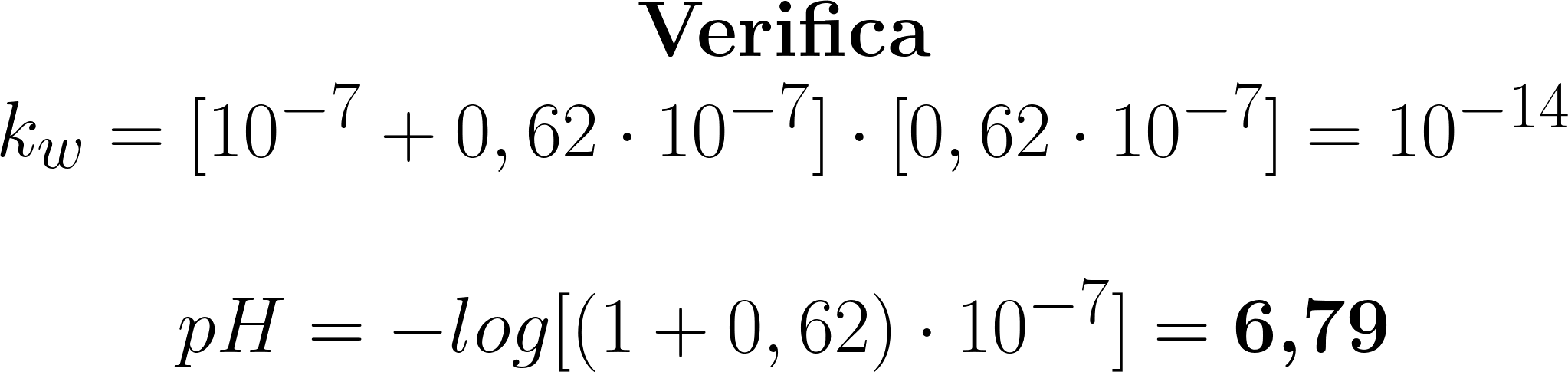
Considerando la somma di ione idronio proveniente
da un acido debole (l’acqua) e da un acido forte molto
diluito, fra 6,30 e 6,79 il più sicuro è il secondo.
BASE POLIFUNZIONALE – EQUILIBRIO SIMULTANEO
Una soluzione è composta da carbonato di sodio
0,05 M, che venga determinato il pH.
\small \begin{matrix} \!\!\!\!\!\!\!\!\!\!\!\!\!CO_{3}^{2-}\!\rightleftharpoons \!HCO_{3}^{-}\;Kb_{1}\!=\!2,10\!\cdot \!10^{-4}\\ \\ \!\!\!\!\!\!\!\!\!\!\!\!\!HCO_{3}^{-}\!\rightleftharpoons \!H_{2}CO_{3} \;Kb_{2}\!=\!2,4\!\cdot \!{\color{Red} 10^{-8}}\\ \textbf{si trascura } \end{matrix}
\begin{matrix} \!\!\!\!\!\!Kb\!=\!\frac{[OH^{-}]\!\cdot \![HCO_{3}^{-}]}{[CO_{3}^{2-}]\!-\!X}\\ \\ \!\!\!\!\!\!\!Kb\!=\!\frac{[X^{2}]}{C-X}\\ \\ \!\!\!\!\!\!\!X^{2}+X(Kb)\!-\!(CKb)\!=\!0\\ \\ \!\!\!\!\!\!\!X_{1}^{2}\!=\!\frac{-Kb\pm \sqrt{Kb^{2}\!+\!4CKb}}{2} \end{matrix}
\begin{matrix} \!\!\!\!\!\!X\!=\!3,1\!\cdot \!10^{-3}M\\ \\ \!\!\!\!\!\!\!\!\!\!pH\!=\!14\!+\!log(10^{-3})\!=\!\textbf{11,5} \end{matrix}
