ESERCIZIARIO ACIDO-BASE

Erman.989
ESERCIZIARIO ACIDO-BASE

Questo articolo è un eserciziario acido-base
di approfondimento del sito di phikipedia.
Si veda l’articolo precedente: acidi e basi deboli.

Prendiamo 13 specie ciascuna 10 molare, o 10
moli. Tali specie devono avere una costante di
reazione che va da 0,11 a salire.

Si ricordi che la costante di reazione equivale
al rapporto moli prodotte/moli reagente all’equilibrio,

il grado di dissociazione, invece, equivale al
rapporto moli prodotte/moli iniziali e la resa al
rapporto percentuale di specie prodotta su specie iniziale.

Ora, proviamo a costruire una tabella immaginando
che le Keq si rifanno a specie monoprotiche e che
forniscano un unico prodotto.

Per intenderci:

\large \!\!\! \begin{matrix} \textit{QUESTO:}\\ K_{eq}=\frac{X}{C-X}\\ \\ \textit{E NON QUESTO:}\\ K_{eq}=\frac{X^{2}}{C-X} \end{matrix}

Keq \frac{p_{eq}}{r_{eq}}{\displaystyle {\boldsymbol {\alpha }}} \frac{n_{f}}{n_{i}}Resa \frac{n_{f}}{n_{i}}\cdot (100)
\frac{1}{10-1}=0,1\bar{1} \frac{1}{10}=0,1 \frac{1}{10}\cdot (100)=10%
\frac{2}{10-2}=0,25 \frac{2}{10}=0,2 \frac{2}{10}\cdot (100)=20%
\frac{3}{10-3}=0,43\frac{3}{10}=0,3 \frac{3}{10}\cdot (100)=30%
\frac{4}{10-4}=0,6\bar{6}\frac{4}{10}=0,4 \frac{4}{10}\cdot (100)=40%
\frac{5}{10-5}=1 \frac{5}{10}=0,5 \frac{5}{10}\cdot (100)=50%
\frac{6}{10-6}=1,5 \frac{6}{10}=0,6 \frac{6}{10}\cdot (100)=60%
\frac{7}{10-7}=2,3\bar{3} \frac{7}{10}=0,7 \frac{7}{10}\cdot (100)=70%
\frac{8}{10-8}=4 \frac{8}{10}=0,8 \frac{8}{10}\cdot (100)=80%
\frac{9}{10-9}=9 \frac{9}{10}=0,9 \frac{9}{10}\cdot (100)=90%
\frac{9,9}{10-9,9}=99 \frac{9,9}{10}=0,99 \frac{9,9}{10}\cdot (100)=99%
\frac{9,99}{10-9,99}=999 \frac{9,99}{10}=0,999 \frac{9,99}{10}\cdot (100)=99,9%
\frac{9,999}{10-9,999}=9.999 \frac{9,999}{10}=0,9999 \frac{9,999}{10}\cdot (100)=99,99%
\frac{10}{10-10}\to \infty \frac{10}{10}=1 \frac{10}{10}\cdot (100)=100%
“tende ad infinito” mai “=” in quanto infinito non è un numero

Non esiste una reazione al 100% di resa, poiché al
grado di dissociazione unitario corrisponderebbe
una costante di equilibrio di reazione infinita.

Lo stesso discorso vale anche per le specie che
dissociano in due specie o più specie (X2 o X3 ecc…).

Keq \frac{p_{eq}}{r_{eq}}{\displaystyle {\boldsymbol {\alpha }}} \frac{n_{f}}{n_{i}}Resa \frac{n_{f}}{n_{i}}\cdot (100)
\frac{1^{2}}{10-1}=0,1\bar{1} \frac{1}{10}=0,1 \frac{1}{10}\cdot (100)=10%
\frac{5^{2}}{10-5}=5 \frac{5}{10}=0,5 \frac{5}{10}\cdot (100)=50%
\frac{9,999^{2}}{10-9,999}=99,980\cdot 10^{6} \frac{9,999}{10}=0,9999 \frac{9,999}{10}\cdot (100)=99,99%
\frac{10^{2}}{10-9,999}\to \infty \frac{10}{10}=1 \frac{10}{10}\cdot (100)=100%
maggiore è l’esponente, più rapidamente tendono all’infinito

ESERCIZIARIO ACIDO-BASE –
ACIDI E BASI FORTI

1) Sia data una soluzione acquosa di acido nitrico
0,100 M. Data la Ka = 20 si determini il valore di pH.

\large \!\!\! \!\!\! \!\!\! \begin{matrix} \!\! HNO_{3}\!\to \!H^{+}\!+\!NO_{3}^{-}\\ \\ \frac{[H^{+}]\!\cdot \![NO_{3}^{-}]}{[HNO_{3}]}\!=\!20\\ \\ \frac{X^{2}}{0,100\!-\!X}\!=\!20\\ \\ X^{2}\!+\!20X-2\!=\!0\\ \\ X_{\frac{1}{2}}\!=\!\frac{-20\pm \sqrt{408}}{2}\!=\!0,095 \end{matrix}

Risolvere l’equazione di II° con gli acidi forti è inutile perché:

\!\!\!\large\begin{matrix} \frac{0,095}{0,100-0,095}=20\\ \\ \frac{0,095}{0,005}=20\\ \\ 0,005\approx 0\\ \\ [HNO_{3}]_{i}=[H^{+}]_{f} \end{matrix}

\large \!\!\!\!\!\!\!\!\!\begin{matrix} ph:\\ \\ -log(H^{+})=\\ \\ -log(0,100)=\\ \\ =-log(10^{-1})=1 \end{matrix}

2) Si calcoli il pH e pOH dell’idrossido di potassio
(KOH) 5,36×10-2 M

\!\!\!\!\!\!\!\!\!\! \begin{matrix} pOH=-log[OH^{-}]\\ \\ pH=14-pOH\\ \\ pH=14+log[5,36\cdot 10^{-2}] \end{matrix}

\large\begin{matrix} pH=12,73\\ \\ pOH=1,27 \end{matrix}

3) Si calcoli il pH ed il pOH di una soluzione acquosa
composta da 0,150 l di acido perclorico (HClO4) 0,45 M
e da 0,250 l 0,100 M dello stesso acido.

\!\!\!\!\!\!\!\!\! \begin{matrix} [H^{+}]:\\ \\ \frac{(0,45\frac{mol}{\not l}\cdot 0,150)\not l+(0,100\frac{mol}{\not l}\cdot 0,250)\not l}{(0,150+0,250)l} \end{matrix}

\large \!\!\!\!\!\!\!\!\!\begin{matrix} [H^{+}]=\frac{(0,0675+0,025)mol}{(0,400)l}\\ \\ [H^{+}]=0,231\, M\\ \\ pH=-log(0,231)\\ \end{matrix}

\!\!\!\!\!\!\!\!\! \begin{matrix} pH=13,36\\ \\ \!pOH=14-13,36=0,64 \end{matrix}

ACIDO-BASE E LE SOLUZIONI

4) Una soluzione di acido cloridrico (HCl) ha
pH =3,50. Aggiungendo X L di HClO4 71%W

1,680 kg/l il pH scende a 1,50. Si calcoli il
volume di acido perclorico.

\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} pH=-log[H^{+}]\\ \\ 10^{pH}=10^{-log[H^{+}]}=-[H^{+}]\\ \\ [H^{+}]=10^{-pH}\\ \\ 10^{-3,5}=3,16\cdot 10^{-4}\, M\\ \\ 10^{-1,5}=3,16\cdot 10^{-2}\, M \end{matrix}

Abbiamo calcolato le concentrazioni iniziali
e finali di ione idronio. Dobbiamo ora considerare
la densità e la percentuale in peso:

\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \frac{Kg_{(HCLO_{4}+H_{2}O)}}{L_{(soluzione})}\!=\!1,680\!=\!1.680\frac{g}{L}\\ \\ \!\!\!\frac{g_{(HCLO_{4})}}{g_{(H_{2}O+HCLO_{4})}}\!\cdot \!(100)\!=\!71\%\\ \end{matrix}

Dal concetto di densità:
1680 g di soluzione occupano un litro.

Percentuale in massa significa:
della soluzione, il 71% in peso
è HClO4. Bisogna calcolare il 71% di 1680:

\!\!\!\!\!\!\!\!\!\begin{matrix} 1680\frac{g}{L} : 100\% = X:71\%\\ \\ \frac{1680\cdot 71}{100}=1192,8\frac{g}{L}\\ \\ \frac{1192,8\frac{{\color{Red}g }}{L}}{100,5\frac{{\color{Red}g}}{mol}}=11,86\, M \end{matrix}

Analogamente, si può fare in un altro modo:

\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \frac{g_{(HCLO_{4})}}{g_{(H_{2}O+HCLO_{4})}}\cdot 100=71\\ \\ 0,71=\frac{g_{(HCLO_{4})}}{g_{(H_{2}O+HCLO_{4})}}\\ \\ \frac{{\color{Red} g_{(HCLO_{4}+H_{2}O)}}}{L_{(soluzione)}}\cdot \frac{g_{(HCLO_{4})}}{\color{Red} g_{(HCLO_{4}+H_{2}O)}}\\ \\ \frac{g_{(HCLO_{4})}}{L_{(soluzione)}}\\ \\ \frac{g_{(HCLO_{4})}}{L_{(soluzione)}\cdot (Pm)}\\ \\ \frac{1680({\color{Red}g })\cdot 0,71}{L_{(soluzione)}\cdot (100,5)\frac{{\color{Red}g }}{mol}}=11,86\, M \end{matrix}

La formula rapida è questa:
(d)(%w)/Pm=[]
densità per percentuale in peso del soluto
diviso il peso molecolare del soluto uguale
alla molarità.

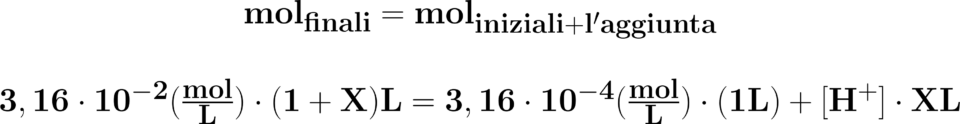
ESERCIZIARIO ACIDO-BASE

La concentrazione finale per il volume
iniziale più quello aggiunto di acido
perclorico è uguale alla concentrazione

inziale per un litro più la concentrazione
di acido perclorico per il suo volume.

In pratica, moli uguali a moli. Non è
possibile calcolare la concentrazione
di ione idronio dalla sottrazione dei

pH perché i volumi cambiano
(la sottrazione è un operazione
omogenea).

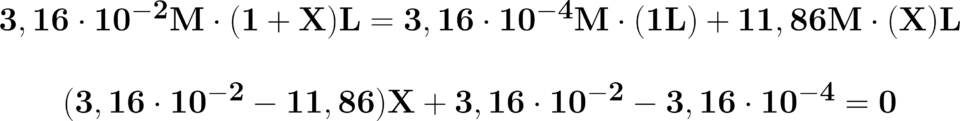
ESERCIZIARIO ACIDO-BASE

\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} -11,83X+0,0313=0\\ \\ X=\frac{0,0313}{11,83}=2,64\cdot 10^{-2}L \end{matrix}

Aggiungendo 2,64 millilitri di
HClO4 71% 1680 g/l il pH scende
da 3,5 a 1,5.

ESERCIZIARIO ACIDO-BASE –
ACIDI E BASI DEBOLI

Questa parte dell’eserciziario acido-base
è la più critica. Va affrontata con calma
e gesso!

1) L’acido acetico ha una costante di
dissociazione acida pari a 1,80×10-5.
Data la concentrazione di 0,100 M
si calcoli il pH.

\small \!\!\!\!\!\!\!\!\!\!\!\begin{matrix} CH_{3}CO_{2}H\!\rightleftharpoons \!CH_{3}CO_{2}^{-}\!+\!H^{+}\\ \\ \!\frac{[CH_{3}CO_{2}^{-}]\!\cdot \![H^{+}]}{[CH_{3}CO_{2}H]}\!=\!1,8\!\cdot \!10^{-5}\\ \\ \!\frac{X^{2}}{0,100-X}\!=\!1,8\!\cdot \!10^{-5} \end{matrix}

Ora, arrivati a questo punto, bisogna
valutare due parametri: la Ka e la C.

Se la Ka è più piccola di 0,0001 (10-4)
e C è maggiore di 0,01 (10-2) allora C-X ≈ C.

0,1 M > 0,01 (10-2) M
1,80×10-5<10-4

\small \!\!\!\!\!\!\!\!\! \begin{matrix} X^{2}+KaX-CKa=0\\ \\ X_{\frac{1}{2}}=\frac{-Ka\pm \sqrt{Ka^{2}+4CKa}}{2}=\\ 1,33\cdot 10^{-3}\\ \\ \!\!pH\!=\!-log[1,33\!\cdot \!10^{-3}]\!=\!2,8\textbf{8}\\ \end{matrix}

\small \!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} X_{\frac{1}{2}}\!=\!\frac{X^{2}}{0,100-X}\!\approx \!\frac{X^{2}}{0,100}\!=\!1,8\!\cdot \!10^{-5}\\ \\ \!\!\!X\!=\!\sqrt{Ka\cdot C}\!=\!1,34\!\cdot \!10^{-3}\\ \\ \!\!pH\!=\!-log[1,34\!\cdot \!10^{-3}]\!=\!2,8\textbf{7} \end{matrix}

2) Data la reazione di equilibrio
dell’ammoniaca pari a 1,85×10-5
si calcoli il pH avendo una
concentrazione 0,550 M.

Come prima guardiamo C e Kb:
5,5×10-1 M > 0,01 (10-2) M
1,85×10-5<10-4

\!\!\!\!\!\!\!\!\!\!\!\!\begin{matrix} NH_{3}\rightleftharpoons NH_{4}^{+}+OH^{-}\\ \\ \frac{X^{2}}{C-X}=1,85\cdot 10^{-5}\\ \\ X_{\frac{1}{2}}=\frac{-Kb\pm \sqrt{Kb^{2}+4CKb}}{2}=\\ =3,1805\cdot 10^{-3}\\ \\ pH:\\ 14+log[3,1805\cdot 10^{-3}]=\\ =11,50\textbf{37} \end{matrix}

\small \!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} X_{\frac{1}{2}}=\sqrt{Kb\cdot C}=3,189\cdot 10^{-3}\\ \\ pH:\\ 14+log[3,189\cdot 10^{-3}]=\\ 11,50\textbf{36}\\ \end{matrix}

3) 100 cm3 0,60 M di acido perclorico
sono mescolati a 100 cm3 0,100 M di
ammoniaca. Si calcoli il pH risultante.

\large \!\!\!\!\!\!\!\!\!\!\begin{matrix} NH_{3}\rightleftharpoons NH_{4}^{+}+OH^{-}\\ \\ HClO_{4} \rightleftharpoons ClO_{4}^{-}+H^{+} \end{matrix}

\!\!\!\!\!\!\!\!\!\!\!\!\footnotesize \begin{matrix} NEUTRALIZZAZIONE: \\ NH_{3}\!+\!HClO_{4}\! \rightleftharpoons \!NH_{4}^{+}\!+\!ClO_{4}^{-}\!+\!H_{2}O \end{matrix}

Ora dobbiamo calcolare la specie
predominante:

\!\!\!\!\!\!\!\!\!\footnotesize \begin{matrix} 100cm^{3}\cdot \frac{1l}{10^{3}cm^{3}}=0,1l\\ \\ \frac{mol_{NH_{3}}-mol_{HClO_{4}}}{V_{tot}}\\ \\ \frac{(0,600\frac{mol}{l})(0,1l)-(0,10\frac{mol}{l})(0,1l)}{0,2l}\\ \\ \frac{0,1{\color{Red} l}}{0,2{\color{Red} l}}(0,600\!-\!0,10)\frac{mol}{l}\!=\!0,25\, M \end{matrix}

Ovviamente, teoricamente lo ione
ammonio cede ioni idronio. Tuttavia,
è inutile imbastire un equazione

di II° visto che contribuisce di un
miliardesimo! pH=-log (0,25)=0,60

GRADO DI DISSOCIAZIONE

TROVARE IL GRADO DI DISSOCIAZIONE

1) Una soluzione acquosa di acido acetico
HAc 0,100 M ha una Ka 1,8×10-5. Si calcoli
il grado di dissociazione.

\large \begin{matrix} \frac{[Ac^{-}]\cdot [H^{+}]}{[HAc]}=Ka\\ \\ \frac{[X^{2}]}{[C-X]}=Ka\\ \\ \alpha =\frac{X}{C}\\ \end{matrix}

\!\!\!\!\!\!\!\!\! \begin{matrix} [C-X]=C(1-\alpha)\\ \\ [X^{2}]=(C\cdot \alpha )^{2} \end{matrix}

Ora va impostato il sistema di
secondo grado:

\footnotesize \!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \frac{(C\cdot \alpha )^{2}}{C(1-\alpha)}=Ka\\ \\ (C\cdot \alpha)^{2}=Ka\cdot C(1-\alpha)\\ \\ (C\cdot \alpha)^{2}+(CKa\alpha)-C\cdot Ka=0\\ \\ (C)(\alpha)^{2}+Ka(\alpha)-Ka=0\\ \\ \alpha_{2}^{1}=\frac{-Ka\pm \sqrt{Ka^{2}+4\cdot C\cdot Ka}}{2C}\\ \\ \alpha=1,33\cdot 10^{-2} \end{matrix}

2) Una soluzione acquosa di ammoniaca
0,550 M ha Kb 1,85×10-5. Si determini il
grado di dissociazione.

\footnotesize \!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \frac{[OH^{-}]\cdot [NH_{4}^{+}]}{[NH_{3}]}=Kb\\ \\ \frac{(C\cdot \alpha )^{2}}{C(1-\alpha)}=Kb\\ \\ (C\cdot \alpha)^{2}=Kb\cdot C(1-\alpha)\\ \\ (C\cdot \alpha)^{2}+(CKb\alpha)-C\cdot Kb=0\\ \\ (C)(\alpha)^{2}+Kb(\alpha)-Kb=0\\ \\ \alpha_{2}^{1}=\frac{-Kb\pm \sqrt{Kb^{2}+4\cdot C\cdot Kb}}{2C}\\ \\ \alpha=5,8\cdot 10^{-3} \end{matrix}

TROVARE IL pH CON LA COSTANTE DI DISSOCIAZIONE

3) Una soluzione di acido benzoico (PhCOOH)
0,050 M ha una costante di dissociazione di

0,085, e la Ka di 3,95×10-4. Si determini il pH
della soluzione.

Schematizzando i dati e le incognite,
matematicamente, diventa:

IMPOSTAZIONE GENERALE

\!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} \frac{[PhCOO^{-}]\cdot [H^{+}]}{[PhCOOH]}=Ka\\ \\ \frac{(C\cdot \alpha )^{2}}{C(1-\alpha)}=Ka\\ \\ \frac{(0,050M\!\cdot \!0,085)^{2}}{(0,050M)(1-0,085)}\!=\!3,95\!\cdot \!10^{-4}\\ \\ pH=X\\ \end{matrix}

Adesso è tutto schematizzato. Per
risolvere l’esercizio si deve ragionare
nel modo seguente:

\footnotesize \!\!\!\!\!\!\!\!\!\!\!\! \begin{matrix} (C\cdot \alpha )^{2}=[PhCOO^{-}]\cdot [H^{+}]\\ \\ (C\cdot \alpha )^{2}=X^{2}=[H^{+}]^{2}\\ \\ X=[H^{+}]\\ \\ pH=-log([H^{+}] )=4,25\cdot 10^{-3} \end{matrix}

Questo è tutto sull’eserciziario acido-base.

– / 5
Grazie per aver votato!

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.